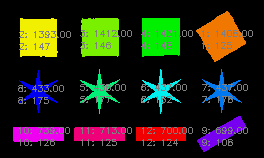
Computing Moments and Features
2020-02-20
Moments are common features that are used in object classification since they are easy to compute.
The moment that is related to the coordinate system is computed as follows
\[ m_{p, q} = \sum\limits_{x} \sum\limits_{y} x^p y^q f(x, y) \, , \] (in our case, we do not have to multiply the coordinates by the corresponding image function, since it is almost the same).
Let us explain some important moments:
The area of an object can be computed as \(m_{0, 0}\).
The center of the mass of an object:
\[ x_t = \frac{m_{1, 0}}{m_{0, 0}}, \quad y_t = \frac{m_{0, 1}}{m_{0, 0}} \, . \]
The circumference of an object may be computed using a simple algorithm that scans each pixel of the object and if the four neighbour of the pixel contains the same values as the central pixel than this pixel does not contribute to the circumference, otherwise it does.
The moment that is related to the center of the mass of an object is computed as follows
\[ \mu_{p, q} = \sum\limits_{x} \sum\limits_{y} (x - x_t)^p (y - y_t)^q f(x, y) \, , \] (in our case, we do not have to multiply the coordinates by the corresponding image function, since it is almost the same).
Features for our Classification
We’ll use two features to describe objects in our images. Let us call them \(F_1\) and \(F_2\). They can be described as follows
\[ F_1 = \frac{\mathrm{Circumference}^2}{100 \mathrm{Area}}, \quad \mathrm{Area} = \mu_{0,0} \]
\[ F_2 = \frac{\mu_{\mathrm{min}}}{\mu_{\mathrm{max}}}, \] where \(\mu_{\mathrm{min}}, \mu_{\mathrm{max}}\) are
\[ \begin{array}{c} \mu_{\mathrm{max}} \\ \mu_{\mathrm{min}} \end{array} = \frac{1}{2} \left( \mu_{2,0} + \mu_{0,2} \right) \pm \frac{1}{2} \sqrt{ 4 \mu_{1,1}^{2} + \left( \mu_{2,0} - \mu_{0,2} \right)^2 }. \]